ASTROMÉTRIE ET ASTRONOMIE FONDAMENTALE

ASTROMÉTRIE ET ASTRONOMIE FONDAMENTALE

L’astrométrie est la partie de l’astronomie qui se propose de déterminer les positions des astres dans le ciel afin de pouvoir interpréter leurs variations dans le temps. Elle est donc la base observationnelle de l’étude dynamique des corps du système solaire, de la cinématique stellaire, de la dynamique galactique. C’est aussi à l’aide d’observations astrométriques qu’on détermine les distances des étoiles par la mesure de leur parallaxe annuelle, qu’on étudie les étoiles doubles et multiples liées par la gravitation, ou bien, encore, qu’on mesure certains phénomènes physiques, comme la déviation des rayons lumineux par un corps massif.

Les observations doivent être rapportées à un système de coordonnées unique, de façon à être directement comparables. D’où l’importance de la notion de repère de référence, dont la définition est l’objectif essentiel de l’astronomie fondamentale. Mais un tel repère n’est pas directement accessible sur le ciel; plusieurs intermédiaires sont nécessaires entre l’observation brute avec un instrument astrométrique et une position dans le ciel dans un tel repère. Pour cela, l’astronomie fondamentale est conduite à définir un certain nombre de systèmes de coordonnées.

Autrefois, la mesure du temps était un autre objectif de l’astronomie fondamentale. Le temps était alors défini à partir de la rotation de la Terre et était déterminé par l’observation d’étoiles à leur passage au méridien (lunette méridienne) ou à un cercle de hauteur (astrolabes). Lorsque les irrégularités de la rotation de la Terre ont été mises en évidence, on a tenté de définir une échelle de temps plus uniforme à partir du mouvement de la Terre autour du Soleil (temps des éphémérides). Mais, entre-temps, les horloges atomiques avaient été inventées, et donnaient une précision et une exactitude bien meilleures. Depuis lors, la seconde est définie à partir d’une fréquence d’oscillation d’un atome de césium ^{[cf. TEMPS]}. L’échelle de temps qui en est déduite est le temps atomique international (T.A.I.) ou le temps universel coordonné (T.U.C., en anglais U.T.C.), qui en diffère d’un nombre entier de secondes pour pouvoir suivre approximativement le temps universel fondé sur la rotation de la Terre (cf. Mouvements de la Terre , in TERRE).

1. Les systèmes de coordonnées

Ne s’intéressant qu’à la direction des astres, l’astrométrie utilise pour repérer ceux-ci des systèmes de coordonnées polaires, chaque astre étant représenté par un point sur la surface d’une sphère de rayon unité. La position de ce point sera repérée par rapport à deux plans perpendiculaires passant par le centre de la sphère, à l’aide des deux angles O OA et A OA ou, ce qui revient au même, des angles sphériques O A et A A (fig. 1). Les calculs faisant intervenir la position des astres s’effectueront alors à l’aide de la trigonométrie sphérique ou en utilisant les matrices de rotation.

Sphère locale, sphère céleste

Pour un observateur terrestre, il est commode de choisir les plans de références fixes par rapport aux objets qui l’entourent. Le plan fondamental le plus aisé à définir est le plan horizontal. Il est déterminé soit par la surface d’un liquide au repos, soit comme plan perpendiculaire à la verticale définie par le fil à plomb. La sphère ainsi définie sera la sphère locale. Le grand cercle du plan horizontal est l’horizon. La verticale ascendante coupe la sphère au zénith Z, et le point diamétralement opposé au zénith est le nadir N.

Par suite du mouvement de rotation de la Terre, les astres ne sont pas fixes sur la sphère locale au cours de la journée. Pour représenter ce mouvement diurne, on suppose l’existence d’une autre sphère, la sphère céleste, qui tourne en glissant sur la sphère locale. Cette rotation, uniforme en première approximation, se fait autour d’un axe appelé axe du monde. Ce dernier coupe la sphère locale au-dessus de l’horizon au pôle céleste P. Lors du mouvement diurne, les astres décriront sur la sphère locale des petits cercles de pôle P. Le plan passant par P et par la verticale du lieu est appelé plan méridien. L’angle qui sous-tend l’arc PN est par définition la latitude astronomique du lieu. Enfin, l’équateur céleste est le grand cercle de pôle P.

Coordonnées horizontales

Dans la sphère locale présentée au paragraphe précédent, on définit les coordonnées horizontales (azimut et distance zénithale). Celles-ci forment un système fixe par rapport à la sphère locale, et dépendent donc de la position de l’observateur à la surface de la Terre.

Soit un astre A sur la sphère céleste (fig. 2). Le grand cercle passant par A et Z est le plan vertical de l’astre. Il coupe l’horizon en A . L’angle SA est l’azimut du point A, noté a . Il est compté de 0 à 360⁰ en allant vers l’ouest. L’angle A A est la hauteur, notée h ; il est compté de 0 à 90⁰, positivement vers le zénith, négativement vers le nadir. La hauteur est souvent remplacée par son complément, la distance zénithale ZA. On définit enfin le cercle de hauteur ou almicantarat de l’astre comme le petit cercle de pôle Z passant par A.

Coordonnées horaires

Les coordonnées horizontales d’un astre ne sont pas constantes. Par suite de la rotation de la Terre, elles varient au cours du temps; les étoiles apparaissent à l’est (lever), s’élèvent dans le ciel puis disparaissent sous l’horizon à l’ouest (coucher). Pour rendre compte de ce mouvement diurne, on définit le système de coordonnées horaires qui sont également des coordonnées locales.

Lors du mouvement diurne, le pôle P et l’équateur céleste sont des éléments invariables de la sphère locale. On peut donc adopter ce dernier comme plan de référence d’un nouveau système de coordonnées (fig. 3).

Le grand cercle PA, cercle horaire de l’astre, coupe l’équateur céleste en A . De même, le plan méridien coupe cet équateur en M. Les coordonnées horaires sont, par définition, les angles MA et A A. L’angle MA est appelé angle horaire de l’astre; il est noté H et est compté conventionnellement en heures et fractions sexagésimales de l’heure, bien qu’il s’agisse là d’un angle et non d’un temps. Aussi a-t-on de plus en plus l’habitude de le compter en degrés, de 0 à 360⁰. Il est compté positivement dans le sens rétrograde, c’est-à-dire vers l’ouest. L’angle A A est la déclinaison, notée 嗀 ; il est compté de 0 à 90⁰, positivement dans la demi-sphère contenant P, négativement dans l’autre. Les petits cercles de pôle P sont les parallèles célestes. Ils représentent les trajectoires des astres au cours du mouvement diurne.

Si on appelle 﨏 la latitude de l’observateur, comptée positivement vers le nord et négativement vers le sud, les relations suivantes lient les coordonnées horizontales et les coordonnées horaires:

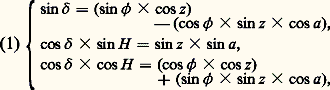ou, inversement:

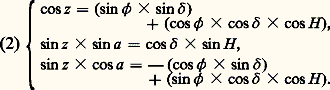Coordonnées équatoriales

La déclinaison d’un astre est la même quel que soit le lieu d’où on l’observe. En revanche, son angle horaire est variable. C’est pour éviter cet inconvénient que l’on définit un troisième système de coordonnées qui est lié à la sphère des fixes.

Le plan de référence choisi est encore l’équateur céleste, et l’une des coordonnées sera, comme dans le système horaire, la déclinaison 嗀 (fig. 4). L’autre, l’ascension droite, est mesurée le long de l’équateur céleste à partir d’un point fixe, le point vernal. L’ascension droite, notée 見 , est comptée en heures et fractions sexagésimales de l’heure, positivement dans le sens direct de 0 à 24 heures, ou encore en degrés de 0 à 360⁰.

Le point vernal est situé sur l’intersection de l’équateur avec l’écliptique, qui est le plan de l’orbite terrestre autour du Soleil ou, ce qui revient au même, le plan du mouvement apparent du Soleil par rapport à la Terre. Des deux points d’intersection, le point vernal (généralement noté 塚) est celui qui est traversé par le Soleil à l’équinoxe de printemps. À cet instant, la déclinaison du Soleil est nulle. L’angle entre l’équateur et l’écliptique est appelé obliquité de l’écliptique. Il vaut environ 23⁰ 27 (cf. tableau).

Temps sidéral

La relation qui lie le système horaire aux coordonnées équatoriales fait intervenir l’angle sur l’équateur céleste entre le point vernal et le plan méridien. On appelle temps sidéral local (T ^l) l’angle horaire du point vernal. On notera que, malgré sa dénomination, c’est un angle et non un temps. Il est directement lié à la rotation de la Terre (cf. Mouvements de la Terre , in TERRE). On considère en général seulement le temps sidéral de Greenwich, noté T ^s, qui est le temps sidéral sur le méridien origine des longitudes. On a dès lors la relation suivante entre l’angle horaire d’un astre et son ascension droite:

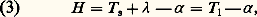où est la longitude géographique de l’observateur, comptée positivement vers l’est.

Notons que, lorsqu’une étoile passe au méridien du lieu, cette relation se simplifie. Prenons l’exemple d’une observation dans l’hémisphère Nord, entre le pôle et le point sud. Son angle horaire est nul, et son ascension droite est égale au temps sidéral local. De même, sa déclinaison vaut 﨏 漣 z au sud du zénith et 﨏 + z entre le zénith et le pôle.

Mouvement des repères

Les repères que nous avons définis, équateur et point vernal, ne sont fixes qu’en première approximation. L’équateur se déplace dans l’espace par suite des couples exercés par la Lune et le Soleil sur le bourrelet équatorial terrestre. L’écliptique, lui, varie par suite des perturbations des planètes sur le mouvement de la Terre. L’ensemble constitue la précession et la nutation. Le nom de précession est réservé aux termes séculaires ou de périodes assez grandes pour être développées suivant les premières puissances du temps t , celui de nutation s’applique aux termes périodiques de courtes périodes ^{[cf. PRÉCESSION ET NUTATION]}.

Par ailleurs, les relations (1) à (3) entre les coordonnées locales et les coordonnées équatoriales ne sont pas immuables. En effet, la latitude du lieu est variable par suite du déplacement des pôles par rapport à des axes rigidement liés à la Terre, alors que le temps sidéral n’est pas proportionnel au temps, mais subit des variations par suite des irrégularités de la rotation de la Terre. Ces quantités, nécessaires pour écrire la transformation, sont déterminées par les observations de la rotation de la Terre.

Systèmes de référence absolus

Les études de dynamique dans le système solaire ou dans la Galaxie ne peuvent se faire en rapportant les mouvements à un repère quelconque. Ainsi, les lois de la dynamique ne sont valables que dans un repère qui ne subit pas d’accélération et, en particulier, ne tourne pas. De même, des études de cinématique donneraient des résultats biaisés si les mouvements étaient rapportés à un système d’axes de coordonnées qui tourne.

On appelle système de référence céleste absolu un système d’axes de coordonnées non tournant. Il y a deux façons de définir un tel système. La première consiste à postuler qu’il est construit de telle façon que les équations qui décrivent les mouvements n’ont pas de terme d’accélération d’entraînement produit par une rotation ou une translation non uniforme. On qualifie de dynamique un tel système. Il est fondé sur la dynamique des corps du système solaire, qui permet de prévoir les mouvements de l’écliptique ainsi que la précession et la nutation, c’est-à-dire, en définitive, prévoir le mouvement du point vernal au cours du temps. On définit actuellement le système de référence dynamique par la position prévisible qu’auront l’équateur et l’écliptique le 1^er janvier de l’an 2000 à midi de Greenwich et noté J 2000,0. La lettre J se réfère ici à la période julienne, composée d’années exactement égales à 365,25 jours. Il faut toutefois noter que cette définition du système de référence dynamique nécessite une modélisation complète du système solaire et l’adoption de nombreux paramètres. Ces valeurs conventionnelles sont réunies dans un tableau appelé système de constantes astronomiques (cf. tableau).

La seconde façon de définir un système de référence céleste non tournant consiste à trouver dans l’Univers des astres qui n’ont pas de mouvement de rotation d’ensemble détectable. C’est le cas des galaxies lointaines et, en particulier, des quasars. Un tel système est dit cinématique . L’Union astronomique internationale a décidé en 1991 que, dans l’avenir, on choisira de se rapporter plutôt à un système cinématique. Il faut pour cela avoir relié avec précision les positions des étoiles et des planètes aux quasars, qui ne sont observables avec précision qu’en ondes radio (cf. infra ). L’origine et les axes d’un tel système sont arbitraires.

Repères de référence absolus

Les systèmes de référence et les axes de coordonnées associés ne sont pas directement accessibles aux instruments d’observation. Il faut y adjoindre des repères dont les coordonnées sont connues par rapport à ces axes. Ces repères sont des étoiles. Le repère de référence dynamique actuel est constitué par un catalogue de 1 535 étoiles appelés FK5 (Fundamental Katalog 5 ). Ce catalogue fournit les positions à l’époque J 2000,0 ainsi que les mouvements propres et les parallaxes permettant de calculer leur position dans le système fondamental à n’importe quelle autre époque. D’autres catalogues donnent la position de nombreuses autres étoiles dans le système du FK5. Ils constituent donc des extensions du repère de référence principal. De même, les éphémérides des planètes et des satellites publiées annuellement donnent les positions de ces astres dans ce système.

L’ensemble des quasars dont on a jusqu’à présent déterminé les positions constitue un repère de référence extragalactique radio qui est pour le moment rattaché au FK5.

2. Réduction d’une observation astrométrique

Une observation astrométrique se ramène en général à la mesure de la position de l’image d’un ou de plusieurs astres sur la surface focale d’un instrument. On appelle réduction de cette observation l’ensemble des calculs qu’il faut effectuer pour obtenir la position de ces astres dans un repère céleste convenable. On peut classer en quatre groupes l’ensemble des transformations qu’il faut faire subir à cette mesure.

Transformation foyer-ciel

L’image d’une portion du ciel dans le plan focal d’un instrument n’est jamais une simple homothétie. Dans le plan focal, l’image a des coordonnées x et y par rapport à une origine, et des directions liées à l’instrument. Sur le ciel, l’astre a des coordonnées différentielles 嗀 et 見 憐 cos 嗀 par rapport à un point central voisin de la direction de visée de cordonnées 嗀 ⁰ et 見 ⁰. La transformation entre x et y , d’une part, 嗀 et 見 憐 cos 嗀 , d’autre part, comprend les diverses perturbations dues à l’instrument (aberrations optiques, déformations mécaniques), la projection de la portion de voûte céleste sur son plan tangent, appelée projection gnomonique, et la déviation des rayons lumineux par l’atmosphère.

L’atmosphère terrestre est un milieu réfringent dont la densité diminue avec l’altitude. Cela a pour effet de modifier la hauteur ou la distance zénithale des astres en relevant toujours la direction apparente. La différence entre la direction réelle et la direction observée à travers l’atmosphère est, par définition, la réfraction astronomique . Elle croît quand la distance zénithale augmente selon la formule de Laplace:

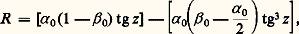formule dans laquelle 見 ⁰ = n ⁰ 漣 1, n ⁰ étant l’indice de réfraction de l’air au niveau du sol et 廓 ⁰ la hauteur qu’aurait une atmosphère homogène de densité égale à celle de l’air au niveau du sol, divisée par le rayon terrestre. Au niveau de la mer, à une température de 0 ⁰C, à une pression normale (760 mm de mercure) et à une longueur d’onde de 0,55 猪m, on a:

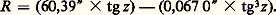En première approximation, R est proportionnel à la pression, inversement proportionnel à la température absolue et augmente lorsque la longueur d’onde diminue.

Dans les calculs de réduction, on prendra en compte la projection gnomonique et la réfraction dans les conditions d’observation. Ce qui reste sera exprimé sous forme d’un développement limité de la forme:

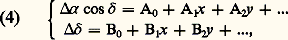où les coefficients A et B sont appelés constantes de la réduction. Leur nombre dépend du champ de l’instrument et de la précision requise pour les résultats.

Déviations des rayons lumineux

Le principal effet dont il faut tenir compte est l’aberration ^{[cf. ABERRATION ASTRONOMIQUE]}, qui est un effet optique dû à la valeur finie de la vitesse de la lumière qui se compose avec la vitesse de l’observateur. Celui-ci ne voit donc pas l’astre dans la direction où il se trouve réellement. On distingue l’aberration annuelle, produite par le mouvement de la Terre autour du Soleil, et l’aberration diurne, due à la rotation de la Terre.

Il faut parfois aussi tenir compte de la déviation des rayons lumineux par des corps massifs. Prévue par la théorie de la relativité générale, cette déviation a pour effet d’écarter la direction apparente de l’étoile du Soleil et vaut:

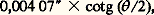où est l’angle entre l’astre et le Soleil.

Changement de système de référence

Si les observations sont faites dans un repère local, les transformations définies par les formules (1) et (3) sont à effectuer en tenant compte en particulier des paramètres de la rotation de la Terre qui modifient la latitude de l’observateur et la relation entre le temps et le temps sidéral. On obtient alors des coordonnées apparentes dans un repère instantané. On appliquera les corrections de nutation et de précession pour se rapporter au système de référence céleste fondamental à l’époque J 2000,0.

Déplacements géométriques

On peut aussi vouloir connaître la direction des astres à partir d’un point fixe, ce qui n’est pas le cas d’un observateur entraîné dans les divers mouvements de la Terre.

La correction de parallaxe est due à la variation de position de l’observateur par suite de la rotation de la Terre (parallaxe diurne) et de son mouvement de révolution autour du Soleil (parallaxe annuelle). La correction de parallaxe est d’autant plus grande que l’astre est rapproché. Elle revient à passer des coordonnées locales (topocentriques), données par l’observation, aux coordonnées géocentriques, par correction de la parallaxe diurne, ou aux coordonnées héliocentriques, par correction de la parallaxe annuelle.

Processus de réduction

Toutes les corrections décrites ci-dessus, sauf les effets instrumentaux, peuvent être exactement calculées. Pour déterminer les constantes de la réduction, on devra inclure parmi les astres observés des étoiles dont on connaît déjà la position. En mesurant leur position au foyer de l’instrument, on pourra déterminer les coefficients A et B des formules (4), et étalonner ainsi l’instrument. On pourra alors calculer 見 憐 cos 嗀 et 嗀 pour les autres astres et on fera subir aux résultats les autres étapes de la réduction.

Cet étalonnage doit être fait à chaque observation, si bien que les observations astrométriques sont systématiquement des observations relatives par rapport à des étoiles de positions connues dans un repère de référence donné. C’est par un processus itératif s’appuyant sur un grand nombre d’observations qu’on améliore les positions des étoiles et des planètes. En rapportant en particulier ces positions aux astres définissant le système de référence (planètes ou quasars), on améliore aussi le repère fondamental lui-même.

3. Instruments et méthodes de l’astrométrie

Les instruments les plus anciens utilisés en astrométrie sont l’armille et le quadrant. En usage jusqu’à la fin du Moyen Âge, ils permirent d’obtenir sur les coordonnées des astres une précision de 梁 2 . En 1689, Olaüs Römer construisit l’instrument des passages qui, avec des perfectionnements, devait être utilisé jusqu’à nos jours sous le nom de lunette méridienne. Sa précision, qui était de l’ordre de 2 au XVIII^e siècle, est passée à 0,40 à la fin du XIX^e siècle et atteint actuellement 0,10 . À la fin du XIX^e siècle, les premières applications de la photographie à l’astrométrie ont conduit à la grande opération mondiale de la Carte du ciel , dont la précision était de l’ordre de 0,30 , alors que l’astrométrie sur des lunettes à long foyer donnait des précisions allant jusqu’à 0,05 vers le milieu du XX^e siècle. Le XX^e siècle a vu successivement apparaître le tube zénithal photographique et l’astrolabe Danjon, essentiellement destinés à l’étude de la rotation de la Terre, et le remplacement des lunettes à long foyer par des télescopes astrométriques. Un saut considérable en précision a été fait grâce à la radio-interférométrie à longue base, puis à l’interférométrie optique et, enfin, à l’astrométrie spatiale, avec le satellite Hipparcos (fig. 5).

La lunette méridienne

L’instrument le plus utilisé pour observer le passage des étoiles est la lunette méridienne, ou cercle méridien. Il est formé d’une lunette d’environ 20 centimètres d’ouverture et de 2 à 4 mètres de distance focale, montée sur un axe fixe horizontal dirigé suivant une ligne est-ouest. Cet axe est formé d’un cube central creux sur lequel se fixent deux tubes coniques terminés par des tourillons cylindriques. Le cube central sert aussi de support pour le tube de la lunette.

Les tourillons sont posés sur des coussinets eux-mêmes portés par des piliers. Ceux-ci sont solidaires l’un de l’autre, et leurs fondations, indépendantes du bâtiment qui abrite la lunette, s’enfoncent profondément dans le sol. Ces précautions assurent une bonne stabilité à la lunette et une bonne reproductibilité dans la direction visée. Toutefois, l’axe optique n’est jamais parfaitement perpendiculaire à l’axe des tourillons, et celui-ci n’est pas exactement orienté est-ouest. Cela introduit respectivement des erreurs de collimation, d’azimut et d’inclinaison qui peuvent atteindre plusieurs secondes d’angle et qu’il faut déterminer à l’aide d’observations d’étoiles de positions connues.

Les meilleurs instruments méridiens actuels sont munis de dispositifs d’observation photoélectriques et sont en général automatiques. Un cercle gradué est solidaire des tourillons. Les lectures sont faites par des dispositifs automatiques de balayage photoélectrique. Au foyer de l’instrument se trouve un chariot qui peut se déplacer avec la vitesse de défilement de l’étoile dans le champ. Il est muni d’un analyseur d’images qui se déplace avec le temps. Au cours de ce déplacement, l’image de l’étoile est partiellement ou totalement occultée selon une loi bien déterminée. Un photomultiplicateur recueille la lumière transmise et l’analyse en fonction du temps. De cette analyse on déduit la correction en déclinaison par rapport au calage des cercles et la correction en ascension droite par rapport à l’origine du mouvement du chariot.

À titre d’exemple, dans l’instrument méridien de Bordeaux (fig. 6), l’analyseur d’images est un demi-cercle qui tourne alors que dans celui de La Palma (îles Canaries) c’est une double fente inclinée à 梁 45⁰ qui a un mouvement de va-et-vient.

Le principe des observations s’inspire des formules données dans la première partie. La direction du zénith est obtenue en plaçant un miroir de mercure sous l’instrument et en notant l’indication du cercle gradué lorsque l’image d’une marque au foyer sur l’axe optique se fait au même point.

La précision des observations est de l’ordre de 0,008 s à 0,010 s en ascension droite et de 0,11 à 0,15 en déclinaison pour ces instruments modernes. Ils peuvent observer des étoiles faibles jusqu’à la magnitude 13 à 14. C’est cette possibilité d’observer avec précision la position des étoiles faibles qui fait l’importance actuelle de ces instruments.

L’astrolabe photoélectrique

Un astrolabe est un instrument qui détermine l’instant de passage d’un astre sur un cercle de distance zénithale donnée, en général 30⁰ ou 45⁰. Nous allons décrire le plus moderne des instruments de ce type: l’astrolabe photoélectrique du C.E.R.G.A. à Grasse (fig. 7). La pièce principale est une équerre optique comprenant une face semi-transparente et une face réfléchissante, toutes deux inclinées par rapport à la verticale d’un angle égal à la distance zénithale d’observation. Alors que la lame semi-transparente renvoie les rayons vers le télescope, la face réfléchissante intérieure reçoit la lumière provenant de la même région du ciel préalablement réfléchie par un miroir de mercure. Il se forme donc deux images au foyer qui coïncident lorsque la distance zénithale de l’étoile est exactement égale à l’inclinaison des lames plus la réfraction (fig. 8).

Avant et après cet instant, les deux images se déplacent sur le plan focal, qui est obstruée par une grille composée de fentes transparentes parallèles. Un photomultiplicateur analyse la lumière transmise par la grille placée de telle façon qu’au plus une seule des images est transmise. Cela permet de déduire la trajectoire de chaque image avec le temps et, par suite, de déterminer l’instant de leur coïncidence.

Lorsqu’une étoile est observée à la fois à son passage est et ouest, on peut déduire des observations son ascension droite et sa déclinaison. Il faut toutefois se servir des observations d’étoiles de positions connues pour affiner la valeur de la réfraction et déterminer les constantes instrumentales, dont la principale est une correction à la distance zénithale d’observation.

L’astrolabe photoéléctrique est un peu plus précis que le méridien, mais ne peut observer que des étoiles brillantes (magnitude inférieure à 8) et, pour constituer un catalogue de positions, il faut systématiquement observer pendant un an un ensemble ne dépassant pas 300 étoiles. L’instrument méridien est beaucoup plus performant quant au nombre d’étoiles pouvant être observées en un an, mais l’astrolabe a pour lui l’avantage que les paramètres instrumentaux sont faibles (de l’ordre de 0,2 à 0,3 ), ce qui lui laisse une plus grande marge d’amélioration dans l’avenir.

L’astrométrie photographique

La mesure des coordonnées des étoiles à l’aide des instruments précédents est une opération longue et ne s’applique qu’aux astres lumineux. Pour étudier un nombre beaucoup plus important d’étoiles, de magnitudes plus faibles, on emploie une méthode photographique.

La plaque photographique est placée au foyer d’une lunette ou d’un télescope équatorial, ce qui permet d’effectuer des poses pour observer des étoiles faibles.

Les positions des images sur la plaque sont mesurées avec une machine à mesurer qui consiste en un châssis mobile sur lequel on fixe la plaque et dont la position est déterminée de façon précise par laser ou par des codeurs incrémentaux. Un réseau de petits récepteurs fixes numérise la transparence d’une petite surface de la plaque placée en face. Un ordinateur analyse alors l’image numérisée de l’étoile et détermine par un algorithme approprié la position du centroïde par rapport à un point fixe du châssis.

On peut remplacer la plaque photographique par un récepteur à transfert de charges (C.C.D., pour charged coupled device ) qui peut être lu électroniquement et donner directement l’image numérisée. Cependant, sa dimension en limite actuellement l’usage à des champs stellaires réduits.

Pour passer des coordonnées sur la plaque aux coordonnées sur le ciel, on procède comme indiqué plus haut. Il faut seulement qu’il y ait sur la plaque suffisamment d’étoiles dont la position est connue. La précision de cette technique est limitée par le nombre suffisant de bonnes références, mais les résultats des mesures effectuées par le satellite Hipparcos devraient permettre une amélioration considérable de la situation.

Deux types de télescopes sont actuellement utilisés pour l’astrométrie photographique. Ce sont d’abord les télescopes de Schmidt ayant un champ de 5⁰ par 5⁰ et dont la précision interne est de l’ordre de 0,15 à 0,25 .

Par ailleurs, des lunettes ou des télescopes à long foyer (de 12 à 18 m), comme le télescope astrométrique de 1,50 m d’ouverture à Flagstaff (États-Unis), ont un champ de l’ordre de un demi-degré et sont utilisés avant tout pour déterminer des parallaxes ou des positions relatives d’étoiles doubles et multiples. Les étoiles voisines servent de repère de référence local pour les nombreux clichés du même champ, et une précision de 0,03 à 0,05 est aisément obtenue.

L’interférométrie optique

Une première application de l’interférométrie optique de Michelson à l’astrométrie a été faite par M. Shao à l’observatoire du mont Wilson en Californie. Deux télescopes visent la même étoile, et on fait converger les deux faisceaux sur le même détecteur. Si les chemins optiques parcourus par les deux faisceaux sont égaux, il se forme des franges de Young sur le détecteur. On montre que, si D est la distance horizontale entre les axes optiques des deux télescopes, h la différence d’altitude, z la distance zénithale de l’étoile et a la différence d’azimut entre la direction de l’étoile et celle des télescopes, la différence de marche est:

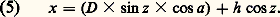Le principe de l’interférométrie optique est de modifier le chemin optique d’un des deux faisceaux et de mesurer cette modification de telle façon que les franges de Young apparaissent, ce qui donne x (fig. 9). En observant l’étoile à divers azimuts, on obtient des relations (5) différentes d’où on peut tirer les coordonnées équatoriales de l’étoile.

La réalisation d’un interféromètre optique astrométrique est très délicate. La distance entre les deux télescopes doit être très stable. Il faut, de plus, mesurer les variations de chemin optique à une fraction de micromètre près. Une autre difficulté consiste à corriger la réfraction. On inclut dans les observations des étoiles du FK5 pour déterminer les constantes instrumentales, après quoi la précision atteinte actuellement est de l’ordre de 0,02 à 0,03 pour une séparation D de l’ordre de 20 mètres. Il semble que 0,01 soit la limite des possibilités de cet instrument qui, par ailleurs, ne peut observer que des étoiles brillantes. Avec les astrolabes photoélectriques, les interféromètres optiques sont les instruments les mieux placés pour maintenir dans l’avenir la qualité du référentiel construit par Hipparcos.

La radio-interférométrie à longue base

Le principe de l’interférométrie est le même pour toutes les ondes électromagnétiques. Cependant, comme le pouvoir de résolution d’un interféromètre est de l’ordre de /D , où est la longueur d’onde, pour avoir une précision importante à des longueurs d’onde centimétriques, les instruments doivent être tellement éloignés l’un de l’autre que l’on ne peut plus ramener les ondes au même détecteur. Aussi, les informations recueillies par chaque radiotélescope sont-elles hétérodynées, puis numérisées et enregistrées sur bande magnétique. La datation est assurée à l’aide d’horloges très stables (masers à hydrogène). Les bandes créées par les deux radiotélescopes subissent un traitement informatique et, par corrélation, on détermine les instants correspondant au même front d’onde. La différence des instants de réception s’interprète comme étant le temps mis par les ondes pour parcourir la différence de chemin optique x .

La base varie avec la rotation de la Terre. Si celle-ci est bien connue par ailleurs, on détermine la position des radiosources. Inversement, connaissant la position des radiosources, on détermine les variations de position de la base, c’est-à-dire les effets de la rotation de la Terre ^{[cf. TERRE]} et la position géographique des stations ^{[cf. GÉODÉSIE]}.

La longueur de la base n’est limitée que par la visibilité simultanée des sources. Elle peut atteindre 8 000 kilomètres. La précision de positionnement des radiosources est de l’ordre de 0,001 5 à 0,001 . Toutefois, en mode différentiel, en comparant les réceptions de deux sources voisines, on obtient des positions encore plus précises.

L’astrométrie spatiale

Il est bien connu que la précision des observations faites par les instruments terrestres est limitée par le caractère fluctuant de l’atmosphère terrestre. D’où l’utilité de faire des observations à partir de satellites artificiels. Cela offre un intérêt considérable pour l’astrométrie et est à l’origine du satellite Hipparcos de l’Agence spatiale européenne lancé le 8 août 1989 (fig. 10).

Conçu sur une idée de Pierre Lacroute (1966), le principe de l’instrument est de faire converger vers le même plan focal deux champs stellaires éloignés et d’analyser l’image complexe du ciel qui est ainsi obtenue. Cela est réalisé par deux demi-miroirs faisant un angle de 29⁰, renvoyant les rayons lumineux sur un télescope. Au foyer se trouvent une grille de 2 688 éléments identiques équidistants et un repéreur d’étoiles formé de quatre fentes parallèles aux éléments de la grille principale et de quatre fentes formant des chevrons inclinés à 45⁰ (fig. 11). Le satellite tourne en 2 heures 8 minutes autour d’un axe parallèle à l’arête du miroir complexe et aux fentes de la grille principale. Un dissecteur d’images, qui est un photomultiplicateur ne prenant en compte que la lumière venant d’une très petite région de la grille, enregistre successivement la modulation de la lumière par la grille principale de chacune des étoiles dans le champ. Des photomultiplicateurs enregistrent également les instants où les images d’étoiles traversent les fentes du repéreur d’étoiles.

Un catalogue des positions approchées des 118 000 étoiles du programme d’observation a été préalablement établi à partir des observations au sol avec une précision moyenne de 0,3 . À partir de ces positions et des observations par le repéreur d’étoiles, on détermine l’orientation du satellite. Celle-ci, jointe aux observations sur la grille principale, permet de déterminer en quelques heures les positions de 1 000 à 1 500 étoiles en projection sur le plan moyen de la rotation avec des précisions allant de 0,003 à 0,017 suivant l’éclat de l’étoile. Le satellite est programmé pour balayer le ciel pendant quatre ans. En combinant les observations ainsi faites sur ces plans, puis en réitérant les calculs pour améliorer la connaissance de l’orientation du satellite, on arrivera à déterminer la position, le mouvement propre annuel et la parallaxe avec des précisions comprises entre 0,001 2 et 0,001 7 pour les étoiles de magnitude inférieure à 9. Les précisions se dégradent rapidement jusqu’à la magnitude 13, limite de sensibilité de l’appareil.

De plus, en analysant systématiquement les temps de passage de toutes les étoiles à travers les grilles du repéreur d’étoiles et en utilisant l’orientation déterminée par la mission principale, on obtiendra la position, le mouvement propre annuel et la parallaxe de quelque 800 000 étoiles avec une précision comprise entre 0,01 et 0,03 . C’est l’expérience Tycho.

Enfin, quelques étoiles ayant des émissions radio sont observées à la fois par Hipparcos et en radio-interférométrie à longue base. Cela permettra de rapporter leurs positions aux quasars et de rattacher ainsi le catalogue Hipparcos au système de référence extragalactique.

Signalons encore que le télescope spatial Hubble peut faire des mesures astrométriques dans trois champs de 4 par 17 avec une précision de l’ordre de 5 millièmes de seconde d’angle.

Encyclopédie Universelle. 2012.